13th Swiss Soft Days at ETH Zurich.

I presented a talk about “Bubbles dancing in a vortex”, and a poster together with Anand and Xevi about “Particle ordering using inertial microfluidics”.

Here is the abstract of my talk:

INTRODUCTION: A feature common to physiological as well as industrial and domestic flow systems is a bifurcation, or T-junction, that split the flow into two symmetric streams. We discovered that, unexpectedly, low-density particles or air bubbles dispersed in the solution can get trapped by the vortical structure that develops at the T-junction. Air bubbles then accumulate and increase in number, eventually changing size due to coalescence.

METHODS: We conduct experiments generating H₂, O₂ or simply air bubbles in the range of Reynolds number, Re = ρvL/μ, where ρ is the fluid density, v the average flow velocity, L the lateral size of the channel and μ the viscosity, between 100 and 5,000, in a variety of T-junction with square section. We explore different lateral size devices ranging from 0.4 to 10 mm, and different air bubbles size. We also performed complete three-dimensional simulations of the pure fluid and the bubbly flow travelling through the T-junction.

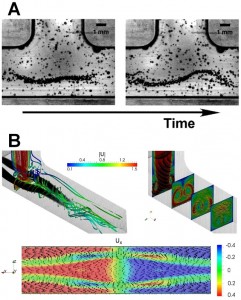
RESULTS: Our experimental analyses revealed different behaviors depending on the Reynolds number. Starting from Re = 100, two symmetrical vortical structures develop at the T-junction. Air bubbles enter the vortices due to centrifugal forces and, surprisingly, for Re > 220, they get trapped, i.e., bubbles that enter the vortices are not leaving the bifurcation and accumulate (see Fig. 1A). For the same flow conditions our numerical simulations show the formation of a pressure gradient, similar to the vortex breakdown, at the core of the vortices directed towards the center of the T-junction. This pressure gradient is the responsible for the trapping phenomenon which is evident by the formation of four symmetric recirculation zones (see Fig. 1B). Bubbles eventually oscillate (i.e. “dance”) in the vortex when the flow becomes unsteady for Re > 550.

We then performed experiments on low-density rigid particles and on pulsed flow similar to physiological conditions, finding again the same trapping mechanism. We also experimentally observed a size dependent behavior of trapping which can be exploited to selectively trap, drag and separate different size of particles.

DISCUSSION & CONCLUSIONS: The ubiquity of the geometry makes the trapping phenomenon that we unveiled extremely relevant for health, diagnostics and safety in industrial processes. In the presence of air bubbles or low-density material dispersed in the carrier fluid, it is important to control the geometry and the flow conditions to avoid or enhance this effect; for example, whenever the presence of a macroscopic air pocket is to be avoided, e.g., while designing a heat exchanger.